
.:: معادله های خطی ::.
معادله خط: (Line equation) رابطه ی بین طول (X) و عرض (Y) نقاط واقع بر یک خط را معادله ی آن خط می گویند که به صورت یک تساوی نوشته می شود .
مثال: به خط L توجه کنید . نقاط ![]() روی این خط قرار دارند .مشاهده می کنیم که طول و عرض این نقاط با هم مساویند . هر نقطه ای که طول و عرض آن مساوی باشد بر خط L قرار می گیرد و هر نقطه ای که روی خط L باشد طول و عرض آن مساوی است.
روی این خط قرار دارند .مشاهده می کنیم که طول و عرض این نقاط با هم مساویند . هر نقطه ای که طول و عرض آن مساوی باشد بر خط L قرار می گیرد و هر نقطه ای که روی خط L باشد طول و عرض آن مساوی است.

اگر طول هر نقطه را با X و عرض آن را با Y نشان دهیم ، رابطه Y=X را معادله ی خط (L) می نامیم. این تساوی، رابطه ی بین طول و عرض نقاط را مشخص می کند.
انواع خط:
در هر یک از تصاویر زیر به خط رسم شده توجه کنید .مختصات نقاط داده شده از خط را بیان کنید و معادله ی خط را بنویسید.
تصویر 1:

حل: 
نکته: این نوع خط ها موازی محور طول ها هستند و معادله ی آن ها به صورت Y=b نوشته می شود . (b یک عدد ثابت برای همه ی نقاط می باشد.)
مانند 1=Y=-2 ، y و ........?
تصویر2:

حل: 
نکته: این نوع خط ها موازی محور عرض ها هستند و معادله ی آن ها به صورت x=a نوشته می شود. (a یک عدد ثابت برای طول همه ی نقاط می باشد.)
مانند 1=X=-2 ، X و ........?
تصویر3:

حل: 
نکته: این نوع خط از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx نوشته می شود.
مانند: ![]()
تصویر 4:

حل: 
نکته: این نوع خط نه موازی محوری است، نه از مبدأ مختصات می گذرد و معادله ی آن به صورت Y=mx+n می با شد. مانند:
![]()
دانش آموزان عزیز: انواع دیگری از خط را که به نظرتان می رسد در یک صفحه ی مختصات رسم کنید و در مورد معادله خط مربوط به هر کدام تحقیق کنید.
صورت استاندارد معادله خط:
هر رابطه ی درجه ی اول بین X و Y مانند: 1-Y=2x و 6=3x+Y را معادله ی خط گو یند صورت استاندارد معادله ی خط Y=mx+n می باشد که در آن m و n دو عدد معلوم و مشخص هستند.صورت دیگر معادله ی خط ax+by=c می باشد که در آن c و b و a سه عدد معلوم می باشند که با هم صفر نیستند و آنرا معادله ی خطی یا معادله ی ضمنی می نامند.
رسم خطی که معادله ی آن داده شده است:
برای رسم یک خط راست به ترتیب زیر عمل می کنیم .
الف:مختصات دو نقطه ی دلخواه آن خط را پیدا می کنیم .
ب:جای این دو نقطه را درصفحه ی مختصات مشخص می کنیم .
ج: این دو نقطه را به هم وصل کرده از دو طرف امتداد می دهیم.
مثال:در هر یک از تصاویر زیر معادله ی یک خط داده شده است. نمودار هر یک از خط های داده شده را رسم کنید.
تصویر 1: Y=?x+?
حل:ابتدا عدد های مختلفی به x می دهیم و عدد های نظیر آن ها را برای y به دست می آوریم.


تصویر 2: x+?y=?
حل:پیشنهاد:در این معادله ،ابتدا به x عدد صفر را می دهیم و جواب نظیر آنرا برای y بدست می آوریم و سپس بر عکس عمل می کنیم ،به yعدد صفر می دهیم و جواب نظیر آنرا برای x بدست می آوریم.

تصویر 3: ![]()
پیشنهاد: در این معادله، ابتدا به X عدد صفر را می دهیم و جواب نظیر آن را برای Y بدست می آوریم و سپس به X عدد 3 را می دهیم، (مخرج کسر) وجواب نظیر آن را برای Y بدست می آوریم.

تصویر 4: ![]()
حل: این معادله را می توانیم به صورت استاندارد بنویسیم و سپس آن را رسم کنیم:

تصویر 5: y=?
حل: این معادله نشان می دهد که عرض همه ی نقاط برابر 3 می باشد.

تصویر 6: X=-?
حل:این معادله نشان می دهد که طول همه ی نقاط برابر 2- می باشد

شیب خط: (gradient of a line)
شیب به معنی سرازیری است (مقابل فراز) و در ریاضیات هر چه زاویه ای که خط با محور افقی می سازد بیشتر باشد ، شیب خط بیشتر است و بر عکس هر چه زاویه ای که خط با محور افقی می سازد کمتر باشد ، شیب خط نیز کمتر است.
در این پارک کدام سرسره شیب بیشتری دارد ؟

در صفحه ی مختصات زیر کدام خط شیب بیشتری دارد؟

با توجه به خط های بالا y=?x بیشترین شیب را دارد در مقایسه ی ضریب x مشاهده می کنیم که ![]() می باشد یعنی: هر چه ضریب x بیشتر باشد شیب خط بیشتر است و هر چه ضریب x کمتر باشد شیب خط کمتر است به طور کلی می توان گفت: اگر معادله ی خطی به صورت y=ax+b نوشته شود، عدد a که ضریب x می باشد، شیب خط نام دارد .
می باشد یعنی: هر چه ضریب x بیشتر باشد شیب خط بیشتر است و هر چه ضریب x کمتر باشد شیب خط کمتر است به طور کلی می توان گفت: اگر معادله ی خطی به صورت y=ax+b نوشته شود، عدد a که ضریب x می باشد، شیب خط نام دارد .
عرض از مبدأ: (y-intercept)
فاصله ای که خط از مبدأ گرفته و محور عرض ها را قطع می کند را عرض از مبدأ خط می گویند.
به عبارت دیگر: عرض نقطه بر خورد خط با محور y ها را عرض از مبدأ گویند.
در صفحه ی مختصات زیر محل بر خورد هر خط با محور عرض ها مشخص شده است.

اکنون نقطه های A و B و C را با معادله ی مربوط به هر خط مقایسه کنید.
![]()
به طور کلی می توان گفت :عدد b در معادله ی y=ax+b را عرض از مبدأ این خط می نامیم .اگر خط از مبدأ مختصات بگذرد عرض از مبدأ آن صفر می شود و معادله ی خط به صورت y=ax در می آید.
 نوشته شده توسط قائد یوسفی در یکشنبه 89/12/1 و ساعت 1:42 عصر | نظرات دیگران()
نوشته شده توسط قائد یوسفی در یکشنبه 89/12/1 و ساعت 1:42 عصر | نظرات دیگران()پادشاه به او مأموریت داده بود راز کار جواهر ساز خیانتکار دربار او را کشف و او را رسوا کند. شاه هیرون بر کار جواهر ساز شک کرده بود و چنین می پنداشت که او بخشی از طلایی را که برای ساختن تاج شاهی به وی داده بود برای خود برداشته و باقی آن را با فلز نقره که بسیار ارزانتر بود مخلوط کرده و تاج را ساخته است. هرچند ارشمیدس می دانست که فلزات گوناگون وزن مخصوص متفاوت دارند ولی او تا آن لحظه این طور فکر می کرد ک مجبور است تاج شاهی را ذوب کند، آن را به صورت شمش طلا قالب ریزی کند تا بتواند وزن آن را با شمش طلای نابی به همان اندازه مقایسه کند. اما در این روش تاج شاهی نیز از بین می رفت، پس او مجبور بود راه دیگری برای این کار بیابد. در آن روز که در خزینه حمام نشسته بود دید که آب خزینه بالاتر آمد و بلافاصله تشخیص داد که بدن او میزان معینی از آب را در خزینه حمام پس زده و جابه جا کرده است.
او با عجله و سراسیمه به خانه بازگشت و شروع به آزمایش عملی این یافته کرد. او چنین اندیشید که اجسام هم اندازه، مقدار آب یکسانی را جابه جا می کنند ولی اگر از نظر وزنی به موضوع نگاه کنیم یک شمش نیم کیلویی طلا کوچکتر از یک شمش نقره به همان وزن است (طلا تقریباً دو برابر نقره وزن دارد) بنابراین باید مقدار کمتری آب را جابه جا کند. این فرضیه ارشمیدس بود و آزمایشهای او این فرضیه را اثبات کرد. او برای این کار نیاز به یک ظرف آب و سه وزنه با وزنهای مساوی داشت که این سه وزنه عبارت بودند از تاج شاهی، هم وزن آن طلای ناب و دوباره هم وزن آن نقره ناب. او در آزمایش خود تشخیص داد که تاج شاهی میزان بیشتری آب را نسبت به شمش طلای هم وزنش پس می راند ولی این میزان آب کمتر از میزان آبی است که شمش نقره هم وزن آن را جابه جا می کند. به این ترتیب ثابت شد که تاج شاهی از طلای ناب و خالص ساخته نشده بلکه جواهر ساز متقلب و خیانتکار آن را از مخلوطی از طلا و نقره ساخته است. به همین ترتیب ارشمیدس یکی از چشمگیرترین رازهای طبیعت را کشف کرد آن هم اینکه می توان وزن اجسام سخت را با کمک مقدار آبی که جابه جا می کنند اندازه گیری کرد. این قانون (وزن مخصوص) را که امروزه چگالی می گویند «اصل ارشمیدس» می نامند. حتی امروز هم هنوز پس از ?? قرن بسیاری از دانشمندان در محاسبات خود متکی به این اصل هستند.
به هر حال ارشمیدس در رشته ریاضیات از ظرفیتهای هوشی بسیار والا و چشمگیری برخوردار بود. او منجنیقهای شگفت آوری برای دفاع از سرزمین خود اختراع کرد که بسیار سودمند افتاد. او توانست سطح و حجم جسمهایی مانند کره، استوانه و مخروط را حساب کند و روش نوینی برای اندازه گیری در دانش ریاضی پدید آورد. همچنین به دست آوردن عدد نیز از کارهای گرانقدر وی است. او کتابهایی درباره خصوصیات و روشهای اندازه گیری اشکال و احجام هندسی از قبیل مخروط منحنی حلزونی و خط مارپیچ، سهمی، سطح کره و استوانه می دانست. علاوه بر آن او قوانینی درباره سطح شیبدار، پیچ اهرم و مرکز ثقل کشف کرد.
ارشمیدس در مورد خودش گفته ای دارد که با وجود گذشت قرنها جاودان مانده و آن اینست: «نقطه اتکایی به من بدهید، من زمین را از جا بلند خواهم کرد.» عین همین اظهار به صورت دیگری در متون ادبی زبان یونانی از قول ارشمیدس نقل شده است اما مفهوم در هر دو صورت یکی است. ارشمیدس هم چون عقاب گوشه گیر و منزوی بود. در جوانی به مصر مسافرت کرد و مدتی در شهر اسکندریه به تحصیل پرداخت و در این شهر دو دوست صمیمی یافت یکی کونون (این شخص ریاضیدان قابلی بود که ارشمیدس چه از لحاظ فکری و چه از نظر شخصی برای وی احترام بسیار داشت) و دیگری اراتوستن که گرچه ریاضیدان لایقی بود اما مردی سطحی به شمار می رفت که برای خویش احترام خارق العاده ای قائل بود.
ارشمیدس با کونون ارتباط و مکاتبه دائمی داشت و قسمت مهم و زیبایی از آثار خویش را در این نامه ها با او در میان گذاشت و بعدها که کونون درگذشت ارشمیدس با دوسته که از شاگردان کونون بود مکاتبه می کرد.
یکی از روشهای نوین ارشمیدس در ریاضیات به دست آوردن عدد پی بود. وی برای محاسبه عدد پی، یعنی نسبت محیط دایره به قطر آن روشی به دست داد و ثابت کرد که عدد محصور ما بین و است. گذشته از آن روشهای مختلف برای تعیین جذر تقریبی اعداد به دست داد و از مطالعه آنها معلوم می شود که وی قبل از ریاضی دان هندی با کسرهای متصل یا مداوم آشنایی داشته است.
در حساب روش غیرعملی و چند عملی یونانیان را- که برای نمایش اعداد ازعلائم متفاوت استفاده می کردند- به کنار گذاشت و پیش خود دستگاه شماری اختراع کرد که به کمک آن ممکن بود هر عدد بزرگی را بنویسیم و بخوانیم.
دانش تعادل مایعات بوسیله ارشمیدس کشف شد و وی توانست قوانین آن را برای تعیین وضع تعادل اجسام غوطه ور به کار ببرد.
همچنین برای اولین بار برخی از اصول مکانیک را به وضوح و دقت بیان کرد و قوانین اهرم را کشف کرد.
در سال ???? ج.ل. هایبرگ مورخ دانشمند و متخصص تاریخ ریاضیات یونانی در شهر قسطنطنیه موفق به کشف مدرک باارزشی شد. این مدرک کتابی است به نام «قضایای مکانیک و روش آنها» که ارشمیدس برای دوست خود اراتوستن فرستاده بود. موضوع این کتاب مقایسه حجم یا سطح نامعلوم شکلی با احجام و سطوح معلوم اشکال دیگر است که بوسیله آن ارشمیدس موفق به تعیین نتایج مطلوب می شد. این روش یکی از عناوین افتخار ارشمیدس است که ما را مجاز می دارد که وی را به مفهوم صاحب فکر جدید و امروزی بدانیم، زیرا وی چیز و هرچیزی را که استفاده از آن به نحوی ممکن بود به کار می برد تا بتواند به مسائلی که ذهن او را مشغول می داشتند حمله ور گردد. دومین نکته ای که ما را مجاز می دارد که عنوان «متجدد» به ارشمیدس بدهیم روشهای محاسبه اوست. وی دو هزار سال قبل از نیوتن و لایب نیتس موفق به اختراع حساب انتگرال شد و حتی در حل یکی از مسائل خویش نکته ای را به کار برد که می توان او را از پیش قدمان فکر ایجاد حساب دیفرانسیل دانست.
زندگی ارشمیدس با آرامش کامل می گذشت همچون زندگی هر ریاضیدان دیگری که تأمین کامل داشته باشد و بتواند همه ممکنات هوش و نبوغ خود را به مرحله اجرا درآورد. زمانی که رومیان در سال ??? قبل از میلاد شهر سیراکوز را به تصرف خود درآوردند سردار رومی مارسلوس دستور داد که هیچ یک از سپاهیانش حق اذیت و آزار و توهین و ضرب و جرح این دانشمند و متفکر مشهور و بزرگ را ندارند با این وجود ارشمیدس قربانی غلبه رومیان بر شهر سیراکوز شد. او به وسیله ی سرباز مست رومی به قتل رسید و این در حالی بود که در میدان بازار شهر در حال اندیشیدن به یک مسئله ریاضی بود. میگویند آخرین کلمات او این بود: دایره های مرا خراب نکن. به این ترتیب بود که زندگی ارشمیدس بزرگترین دانشمند تمام دورانها خاتمه پذیرفت. این ریاضیدان بی دفاع هفتاد و پنج ساله در سال ??? قبل از میلاد به جهان دیگر رفت.
ارشمیدس یکی از بزرگترین دانشمندان ریاضی و مکانیک در عصر خودش بود. پدرش فیدیاس که منجم بود او را برای آموزش از سیراکوز به مدرسه ریاضیات اسکندریه فرستاد. شهر اسکندریه را اسکندر مقدونی در سال 323 ق.م در زمان حمله و حرکت به سوی شرق بر کرانه مدیترانه در خاک مصرساخت. این شهر پس از رکود آتن - پایتخت یونان - مرکز علم و تجارت شد و بزرگانی چوت اقلیدس و بطلمیوس و ارشمیدس را تربیت کرد. این شهر حتی موقعی که به دست مسلمانان فتح شد از مراکز مهم علوم یونانی بود و در انتقال علم و اندیشه یونانی به فرهنگ و تمدن اسلامی نقش مهمی داشت.
درباره خصوصیات زندگی ارشمیدس اطلاعات زیادی در دست نیست. اما علاقه اش به ریاضیات و مسائل علمی مکانیک سبب شده است که کارهای با ارزشی از او باقی بماند. گفته می شود که وقتی به مساله ای علاقمند می شد از خوردن و خفتن غافل می شد و چنان خود را سرگرم کار و حل مشکل می کرد که هر مساله دیگری او را از کار باز نمی داشت.
نمو نه هایی از این ها که به کرات گفته شده ، تاج شاه هیرون و زرگر مورد سوء ظن است. گویا شاه هیرون تاجی زرین داشته و نگران از آن که مبادا در ساختن آن به طور پنهانی نقره به کار رفته باشد ، وی مطلب را به ارشمیدس ارجاع می کند ، که او ، روزی در حال استحمام ، با کشف اولین قانون ئیدروستاتیک به راه حل مسئله دست می یابد . با فراموش کردن این که جامه بر تن کند از حمام بیرون می آید , و در خیابان ها به سوی خانه می دود، در حالی که فریاد می زده : " ایورکا ، ایورکا " یعنی: یافتم , یافتم
ارشمیدس قسمت زیادی از کار هندسه خود را به کمک اشکالی رسم شده در خاکستر یا روغن که بعد از استحمام کردن به تن خود می مالیده انجام می داد .وقتی که ارشمیدس روی شن های ساحل دریا اشکال هندسی خود را رسم کرده بود سربازی بدون توجه با راه رفتن روی شن ها اشکال او را لگد کرد و ارشمیدس چنان اعتراض کرد که موجب خشم سرباز شد و سرباز با شمشیرش به ارشمیدس حمله کرد و او را کشت. از آثار علمی او می توان کشف قانون مایع ها و گازها (معروف به قانون ارشمیدس). تعیین جرم حجمی طلا و نقره و بعضی فلزات دیگر و اختراع پیچ مخصوص حلزونی شکل به نام پیچ ارشمیدس برای بالا بردن آب اشاره کرد.
کشفی در حمام
روزی که او در حمامی عمومی به داخل خزینه پا نهاد و در آن نشست و حین این کار بالا آمدن آب خزینه را مشاهده کرده ، ناگهان فکری به مغزش خطور کرد. او بلافاصله لنگی را به دور خود پیچید و با این شکل و شمایل به سمت خانه روان شد و مرتب فریاد میزد یافتم، یافتم. او چه چیزی را یافته بود؟ پادشاه به او مأموریت داده بود راز جواهر ساز خیانتکار دربار را کشف و او را رسوا کند. شاه هیرون بر کار جواهر ساز شک کرده بود و چنین میپنداشت که او بخشی از طلایی را که برای ساختن تاج شاهی به وی داده بود برای خود برداشته و باقی آن را با فلز نقره که بسیار ارزانتر بود مخلوط کرده و تاج را ساخته است.
هر چند ارشمیدس میدانست که فلزات گوناگون وزن مخصوص متفاوت دارند، ولی او تا آن لحظه اینطور فکر میکرد که مجبور است تاج شاهی را ذوب کند، آنرا به صورت شمش طلا قالب ریزی کند تا بتواند وزن آن را با شمش طلای نابی به همان اندازه مقایسه کند. اما در این روش تاج شاهی از بین میرفت، پس او مجبور بود راه دیگری برای این کار بیابد. در آن روز که در خزینه حمام نشسته بود دید که آب خزینه بالاتر آمد و بلافاصله تشخیص داد که بدن او میزان معینی از آب را در خزینه حمام پس زده و جابجا کرده است.
آزمایش و اثبات ناخالصی تاج شاهی (کشفی از رازهای طبیعت)
او با عجله و سراسیمه به خانه بازگشت و شروع به آزمایش عملی این یافته کرد. او چنین اندیشید که اجسام هم اندازه ، مقار آب یکسانی را جابجا میکنند، ولی اگر از نظر وزنی به موضوع نگاه کنیم یک شمش نیم کیلویی طلا کوچکتر از یک شمش نقره به همان وزن است (طلا تقریبا دو برابر نقره وزن دارد)، بنابراین باید مقدار کمتری آب را جابجا کند. این فرضیه ارشمیدس بود و آزمایشهای او این فرضیه را اثبات کرد. او برای این کار نیاز به یک ظرف آب و سه وزنه با وزنهای مساوی داشت که این سه وزنه عبارت بودند از تاج شاهی ، هم وزن آن طلای ناب و دوباره هم وزن آن نقره ناب.
او در آزمایش خود تشخیص داد که تاج شاهی میزان بیشتری آب را نسبت به شمش طلای هم وزنش پس میراند، ولی این میزان آب کمتر از میزان آبی است که شمش نقره هم وزن آن را جابجا میکند. به این ترتیب ثابت شد که تاج شاهی از طلای ناب و خالص ساخته نشده، بلکه جواهر ساز متقلب و خیانتکار آن را از مخلوطی از طلا و نقره ساخته است و به این ترتیب ارشمیدس یکی از چشمگیرترین رازهای طبیعت را کشف کرد. آن هم اینکه میتوان وزن اجسام سخت را با کمک مقدار آبی که جابجا میکنند اندازه گیری کرد. این قانون (وزن مخصوص) را که امروزه به آن چگالی میگویند اصل ارشمیدس مینامند. حتی امروز هم هنوز پس از 23 قرن بسیاری از دانشمندان در محاسبات خود متکی به این اصل هستند.
.jpg)
پیچ ارشمیدس
فعالیت در حوزههای دیگر
ارشمیدس در رشته ریاضیات از ظرفیتهای هوشی بسیار والا و چشمگیری برخوردار بود. او منجنیقهای شگفت آوری برای دفاع از سرزمینهای خود اختراع کرد که بسیار سودمند افتاد. او توانست سطح و حجم جسمهایی مانند کره ، استوانه و مخروط را حساب کند و روش نوینی برای اندازه گیری در دانش ریاضی پدید آورد. همچنین بدست آوردن عدد نیز از کارهای گرانقدر وی است. او کتابهایی درباره خصوصیات و روشهای اندازه گیری اشکال و احجام هندسی از قبیل مخروط ، منحنی حلزونی و خط مارپیچ ، سهمی ، سطح کره «ماده غذایی» و استوانه نوشته ، علاوه بر آن او قوانینی درباره سطح شیب دار، پیچ ، اهرم و مرکز ثقل کشف کرد.
یکی از روشهای نوین ارشمیدس در ریاضیات بدست آوردن عدد بود، وی برای محاسبه عدد پی ، یعنی نسبت محیط دایره به قطر آن روشی بدست داد و ثابت کرد که عدد محصور مابین 7/1 3 و 71/10 3 است، گذشته از آن روشهای مختلف برای تعیین جذر تقریبی اعداد به دست داد و از مطالعه آنها معلوم میشود که وی قبل از ریاضیدانان هندی با کسرهای متصل یا مداوم متناوب آشنایی داشته است. در حساب روش غیر عملی و چند عملی یونانیان را که برای نمایش اعداد از علائم متفاوت استفاده میکردند، به کنار گذاشت و پیش خود دستگاه شمارشی اختراع کرد که به کمک آن ممکن بود هر عدد بزرگی را بنویسیم و بخوانیم.
دانش تعادل مایعات بوسیله ارشمیدس کشف شد و وی توانست قوانین آنرا برای تعیین وضع تعادل اجسام غوطه ور بکار برد. همچنین برای اولین بار برخی از اصول مکانیک را به وضوح و دقت بیان کرد و قوانین اهرم را کشف کرد.
ارشمیدس و دیگر دانشمندان دوران خود
ارشمیدس در مورد خودش گفتهای دارد که با وجود گذشت قرنها جاودان مانده و آن این است: «نقطه اتکایی به من بدهید، من زمین را از جا بلند خواهم کرد». عین همین اظهار به صورت دیگری در متون ادبی زبان یونانی از قول ارشمیدس نقل شده است، اما مفهوم در هر دو صورت یکی است. ارشمیدس هم چون عقاب گوشه گیر و منزوی بود، در جوانی به مصر مسافرت کرد و مدتی در شهر اسکندریه به تحصیل پرداخت و در این شهر دو دوست قدیمی یافت، یکی کونون (این شخص ریاضیدان قابلی بود که ارشمیدس چه از لحاظ فکری و چه از نظر شخصی برای وی احترام بسیار داشت) و دیگری اراتوستن که گر چه ریاضیدان لایقی بود، اما مردی سطحی به شمار میرفت که برای خویش احترام خارق العادهای قائل بود.
ارشمیدس با کونون ارتباط و مکاتبه دائمی داشت و قسمت مهم و زیبایی از آثار خویش را در این نامهها با او در میان گذاشت و بعدها که کونون در گذشت، ارشمیدس با دوستی که از شارگردان کونون بود مکاتبه میکرد. در سال 1906 ج.ل. هایبرگ مورخ دانشمند و متخصص تاریخ ریاضیات یونانی در شهر قسطنطنیه موفق به کشف مدرک با ارزشی شد.
این مدرک کتابی است به نام قضایای مکانیک و روش آنها که ارشمیدس برای دوست خود اراتوستن فرستاده بود. موضوع این کتاب مقایسه حجم یا سطح نامعلوم شکلی با احجام و سطوح معلوم اشکال دیگر است که بوسیله آن ارشمیدس موفق به تعیین نتیجه مطلوب میشد. این روش یکی از عناوین افتخار ارشمیدس است که ما را مجاز میدارد که وی را به مفهوم صاحب فکر جدید و امروزی بدانیم، زیرا وی همه چیز و هر چیزی را که استفاده از آن به نحوی ممکن بود بکار میبرد تا بتواند به مسائلی که ذهن او را مشغول میداشتند حمله ور گردد.
دومین نکتهای که ما را مجاز میدارد که عنوان متجدد به ارشمیدس بدهیم روشهای محاسبه اوست. وی دو هزار سال قبل از اسحاق نیوتن و لایب نیتس موفق به اختراع حساب انتگرال شد و حتی در حل یکی از مسائل خویش نکتهای را بکار برد که میتوان او را از پیش قدمان فکر ایجاد حساب دیفرانسیل دانست.
نیروی ارشمیدس
آیا تاکنون فکرکرده اید که چرا برخی چیزها درون آب شناور هستند امابرخی دیگر ته آب میافتند؟
یا چرا چوب روی آب شناور ولی یک میخ آهنی ته ظرف آب می افتد و یااینکه آیا امکان دارد یک قطعه آهن شناوربماند تمامی این موضوعات به نیرویی مربوط می شود که ارشمیدس دانشمند یونان باستان کشف کرده است.
نیروی ارشمیدس چیست ؟
وقتی جسمی را درون یک شاره مثلا یک لیوان آب می اندازیم اگر جسم تماما درون آب فرو رود به مقدار حجم خود آب را جابجا می کند به نیروی وزن این مقدار آب جابجا شده نیروی ارشمیدس گویند که همیشه رو به بالاست و از رابطه ی زیر بدست می آید:
دقت کنید که در این رابطه چگالی شاره و vحجم شاره جابجا شده است که مساوی است باحجم قسمتی از جسم که داخل شاره است و gشتاب گرانشی است حال سوالی مطرح می شود و آن اینکه چه شرایطی لازم است تا یک جسم در یک شاره شناور شود ؟ می دانیم در به هر جسمی در یک میدان گرانشی نیروی وزن وارد می شود و به جسم درون شاره حداقل دو نیروی ارشمیدس و نیروی گرانش وارد می شود می دانیم که نیروی گرانش همیشه روبه پایین و نیروی ارشمیدس (نیروی شناوری) همیشه روبه بالا هرگاه این دو نیرو برابر باشند جسم درون آب غوطه ور می شود ولی فرق شناوری و غوطه وری چیست ؟ وقتی می گوییم جسمی شناور است که در سطح آب باشد اما جسم غوطه ور میتواند در هر جای شاره باشدبه طور مثال خود آب درون خود شناور است.
.jpg)
وقتی نیروی ارشمیدس از نیروی وزن بیشتر باشد جسم روی سطح آزاد شاره شناور می شود و وقتی نیروی وزن جسم از نیروی ارشمیدس بیشتر باشد جسم درون شاره غرق می شود.
.jpg)
مثال:آیاجسمی به چگالی 1250 kg/m3 روی آب شناور می ماند؟ و مقدار نیروی ارشمیدس این ماده را برای3 1m از این ماده به دست آورید.
(ب)
.jpg)
مثال (2) نیروی شناوری را برای آهن mکه در جیوه شناور است بدست آورید .
.jpg)
با توجه به اینکه نیروی وزن این قطعه آهن 3.9 اسحاق نیوتن است پس حتی آهن نیز روی جیوه شناور می ماند
.jpg)
مسئله : این دو جسم در هوا روی یک ترازوی این چنین به تعادل می رسند اگر آنها را در یک محفظه خلا بگذاریم موقعیت آنان چگونه است ؟(راهنمایی:هوا نیز یک شاره است)
داستانی از ارشمیدوس
.jpg)
در حمام عمومی شهر، بخار از این سو به آن سو می رفت و هرگاه تازه واردی از راه می رسید موجی از هوای خشک و اندکی معتدل با خود به همراه می آورد و میهمان بدن های عریان حمام کنندگان می کرد. آنگاه هر کسی چشمش را می بست و در فرار از هوای نیمه سرد به آغوش آب گرم خزینه بر می گشت.
ارشمیدس - دانشمند بزرگ یونان باستان - غرق در تفکر در خزینه نشسته بود. چشمش را که بست پادشاه را دید که مجلل و باشکوه به تاج طلای خویش خیره شده بود. پادشاه دستش را پیش آورد و تاج را بر سر گذاشت. سازنده تاج لبخند می زد و پادشاه را می نگریست. پادشاه ناگهان به چیزی مشکوک شد. با فریاد از خودش پرسید:
طلا؟ طلا؟ طلا؟... همه اش از طلا؟...
طلا؟ طلا؟ طلا؟... همه اش از طلا؟...
طلا؟ طلا؟ طلا؟... همه اش از طلا؟...
...
پووووووووووف...
دلاک کاسه آب خنک را روی سر ارشمیدس خالی کرد...
ارشمدیس لرزید، سپس به زیر آب رفت و دوباره بالا آمد... مقداری آب از خزینه بیرون ریخت...
طلا؟ طلا؟ طلا؟... همه اش از طلا؟...
...
ساعتی گذشت...
***
- اورکا! اورکا!
هر کسی که داشت از بازار برای خودش خرید می کرد با شنیدن فریاد های ((یافتم! یافتم)) سرش را برگرداند. ارشمیدس در حالی که لباس بر تن نداشت می دوید و داد و فریاد می کرد...
- اورکا! اورکا!
...
.jpg)
در محضر پادشاه
- چه چیزی را یافته ای ارشمیدس... این چه سر و وضعی است برای خودت درست کرده ای؟... چرا لباس بر تن نداری؟!
- جناب پادشاه... یافتم!... حل مسئله را یافتم... آهنگر متقلب در میان تاج طلای شما نقره به کار برده است!
- چگونه فهمیدی؟ از کجا مطمئنی؟ تو که درون تاج ما را ندیده ای ارشمیدس!
تجزیه و تحلیل ایستایی سیالات
قانون ارشمیدس: هر جسمی که در آب قرار گیرد به اندازه ی آبِ هم حجمِ خودش سبک تر می شود.
بنابراین با دانستن اینکه وزن مخصوص طلا و نقره متفاوت است ارشمیدس معمای تاج طلای پادشاه را حل کرد و قانونی را در مکانیک سیالات بنا نهاد...
در ساحل بندر سیراکوز مردم زیادی جمع شده بودند. عده ای به خواسته ارشمیدس روی یک کشتی باری تجمع کرده بودند و در ضمن ارشمیدس کشتی را پر از بار کرده بود. او می خواست ادعای عجیب خود را ثابت کند که: من می توانم با نیروی دست خود این کشتی را حرکت دهم!
ارشمیدس یک سر اهرم بلند خود را زیر کشتی، نزدیک به همان انتها را روی گوه و انتهای بسیار دور دیگر را در دست خود گرفته بود. جمعیت و پادشاه به نظاره ایستاده بودند. ارشمیدس دست خود را بالا برد تا توجه همگاه را جلب کند. آنگاه با دستش نیروی کمی به اهرم وارد کرد و... کشتی به حرکت درآمد!
پادشاه از تعجب آه کشید و صدای همهمه فراگیر شد. همگان برای ارشمیدس دست زدند. ارشمیدس در حالیکه متواضعانه گام برمی داشت نزد پادشاه آمد.
- از تو معجزه زیاد دیده ایم... چگونه این کار را کردی ارشمیدس؟
- معجزه نبود حضرت والا. علم بود... من حتی می توانم با علم خویش زمین را هم حرکت دهم!!
- زمین راااااا؟!!!
- بله حضرت والا... به شرطی که تکیه گاهی مانند آن گوه به من بدهید!
.jpg)
مباحث فیزیک مکانیک صلبیات
قانون گشتاور: هر قدر بازوی گشتاور بلند باشد اعمال تغییر مکان با نیروی کوچتری امکان پذیر است.
.jpg)
سواری سرگردان در میدان جنگ می گشت. هماوردش را یافت و تاخت کنان به سمت او آمد. شمشیر را بالا گرفت و بر سپر او کوبید. حریفش امانش نداد و با نیزه از خود دورش کرد. سرباز دیگری کمی آن طرف تر در خاک غلطید. از میدان نبرد، بخار غلیظ خون بلند می شد. سیراکوز اسیر هجوم مهاجمان شده بود و از خود دفاع جانانه ای می کرد. آن سو تر سه سرباز کمند آتش افکن ساخته دست ارشمیدس را کشیدند و گلوله ای آتش به سمت دشمن پرتاب کردند. گلوله آتش به فاصله کمی از یک کشتی جنگی مهاجم به کام دریا رفت. سربازان گلوله دیگری در منجنیق گذاشتند. در هیاهوی نبرد دانشمند پیر شهر، هندسه دان و فیزیک دان بزرگ، ارشمیدس روی زمین نشسته بود و مشغول حل مسئله هندسه ای بود که با چوب روی خاک کشیده بود. سربازی به تاخت نزدیک شد. دانشمند به یکباره ترسید. سوار قصد جانش را کرده بود. ارشمیدس فریاد زد: نزدیک نیا... هر کاری می خواهی بکن... اما به این مسئله دست نزن... دست نزن...
برق خشم از چشمانش می بارید...
سرباز دشمن شمشیرش را بالا برد...
و مغلوبانه بر روی مسئله هندسی تاخت...
منابع :
ارشمیدس http://daneshnameh.roshd.ir
ارشمیدس http://www.ajayeb.ir
نیروی ارشمیدس http://edu.tebyan.net
نیروی ارشمیدس http://daneshnameh.roshd.ir
ارشمیدس http://www.academist.ir
ارشمیدس http://natali123.persianblog.ir
/خ
 نوشته شده توسط قائد یوسفی در یکشنبه 89/11/24 و ساعت 3:55 عصر | نظرات دیگران()
نوشته شده توسط قائد یوسفی در یکشنبه 89/11/24 و ساعت 3:55 عصر | نظرات دیگران()پس در کل از اینکه  باشد ، به این نتیجه رسیدیم که a و b بایستی اعداد زوجی باشند که در این صورت a و b دارای حداقل یک مقسوم علیه مشترک ( یعنی 2 ) هستند که این نتیجه با فرض اولیه ی ما ( a و b هیچ مقسوم علیه مشترکی ندارند ) در تناقض است . یعنی
باشد ، به این نتیجه رسیدیم که a و b بایستی اعداد زوجی باشند که در این صورت a و b دارای حداقل یک مقسوم علیه مشترک ( یعنی 2 ) هستند که این نتیجه با فرض اولیه ی ما ( a و b هیچ مقسوم علیه مشترکی ندارند ) در تناقض است . یعنی  عددی گنگ است . »
عددی گنگ است . »
بر گرفته شده از http://www.sinuous83.com/index.php?option=com_content&task=view&id=294&Itemid=99999999
با عرض سلام به شما دوستان عزیز از اینکه این اثبات کوچک را در دو پست ارسال کرده ام پوزش می خواهم.
(بدلیل اشکال در سیستم وبلاگ)
 نوشته شده توسط قائد یوسفی در یکشنبه 89/11/24 و ساعت 3:35 عصر | نظرات دیگران()
نوشته شده توسط قائد یوسفی در یکشنبه 89/11/24 و ساعت 3:35 عصر | نظرات دیگران()« فرض کنیم  کسری با کوچکترین جملات است که در آن a و b هیچ مقسوم علیه مشترکی ندارند. فرض کنیم
کسری با کوچکترین جملات است که در آن a و b هیچ مقسوم علیه مشترکی ندارند. فرض کنیم  . دو طرف تساوی را به توان 2 می رسانیم :
. دو طرف تساوی را به توان 2 می رسانیم :  بنابراین
بنابراین  . یعنی
. یعنی  عددی زوج است . چون توان دوم هر عدد فرد، عددی فرد است پس چون
عددی زوج است . چون توان دوم هر عدد فرد، عددی فرد است پس چون  زوج است ، a نمی تواند عددی فرد باشد ؛ پس a زوج است و می توان فرض کرد a = 2k . بنابراین
زوج است ، a نمی تواند عددی فرد باشد ؛ پس a زوج است و می توان فرض کرد a = 2k . بنابراین  که نشان می دهد
که نشان می دهد  . پس
. پس  زوج است و b نیز زوج خواهد شد.
زوج است و b نیز زوج خواهد شد.
 نوشته شده توسط قائد یوسفی در یکشنبه 89/11/24 و ساعت 3:28 عصر | نظرات دیگران()
نوشته شده توسط قائد یوسفی در یکشنبه 89/11/24 و ساعت 3:28 عصر | نظرات دیگران()قضیه
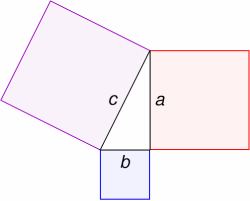 |
د رمثلث قائمالزاویه ABC که زاویه A در آن قائمه است ، در صفحه رابطهی زیر همیشه بین اضلاع برقرار است:
 |
میتوان این قضیه را به صورت سادهتر بیان کرد : فرض کنید سه مربع روی اضلاع یک مثلث قائم الزاویه،که طول اضلاع قائم آن a وb و طول وتر آن c میباشد؛مطابق شکل زیر میسازیم
این قضیه به ما توضیح میدهد که جمع مساحتهای دو مربع ساخته شده روی دو ضلع قائم یک مثلث قائم الزاویه با مساحت مربع ساخته شده روی وتر برابر است.
مثلث قائم الزاویه مثلثی است که دارای یک زاویه قائم میباشد و به ضلعی که روبروی این زاویه در مثلث قرار دارد، وتر میگویند.
در شکل اضلاع زاویه قائم با aوb و وتر با c نشان داده شده است.
بیان دیگر قضیه به این صورت است که در یک مثلث قائم الزاویه مجموع مربعات دو ضلع قائم با مجذور وتر برابر است.
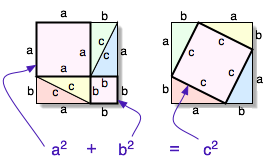 |
می توان با توجه به شکل روبرو اثبات هندسی قضیه را به راحتی درک کرد.
در هر دو شکل مربعی به ضلع a+b داریم.در شکل سمت راست چهار نمونه از مثلث قائم الزاویه دور مربع ساخته شده بروی وتر وجود دارد. و هر چهار مثلث دارای مساحت یکسان می باشند. با چند جابجایی در شکل سمت راست به شکل سمت چپ میرسیم.در این شکل همان چهار مثلث قبلی وجود دارند ولی مربعی که اضلاع آن به c بود به دو مربع به اضلاع a,b تبدیل شده است، که همان قضیه فیثاغورث را نشان میدهد



 نوشته شده توسط قائد یوسفی در دوشنبه 89/11/11 و ساعت 4:53 عصر | نظرات دیگران()
نوشته شده توسط قائد یوسفی در دوشنبه 89/11/11 و ساعت 4:53 عصر | نظرات دیگران()بازدید دیروز: 0
مجموع بازدیدها: 44497
ریاضی با معلم ریاضی [4]
مهدی موعود
کد تقلب همه ی بازی ها
استقلالیا [4]
سایت سازنده ی برنامه های فارسی [1]
مجله ی تخصصی نجوم ایران ـ جالبه - [2]
لغتنامه ی تخصصی کامپیوتر - انگلیسی [2]
سایت تخصصی برای چت بازان حرفه ای !
این سایت مخصوص گزارش وضع هوای .
سایت فارسی کارت های تبریک
تبدیل تاریخ از شمسی به میلادی [1]
جمعیت لحظه ای جهان [2]
[آرشیو(13)]
